数据结构与算法基础内容提要
数组与矩阵
线性表
广义表
树与二叉树
图
排序与查找
算法基础及常见的算法
数组数组类型:存储地址计算
一维数组a[n]:a[i]的存储地址为:a+i*len
二维数组a[m][n]:
a[i][j]的存储地址(按行存储)为:a+(i*n+j)*len
a[i][j]的存储地址(按列存储)为:a+(j*n+i)*len
稀疏矩阵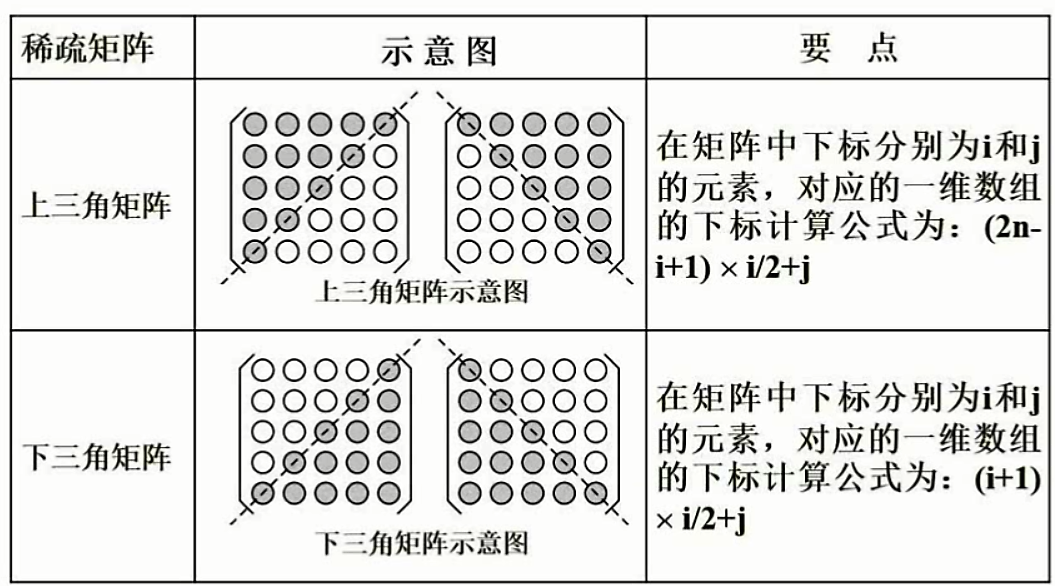
例题


1.数据结构的概念
2.数据逻辑结构
线性结构
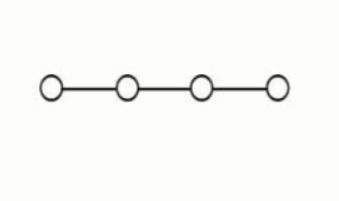
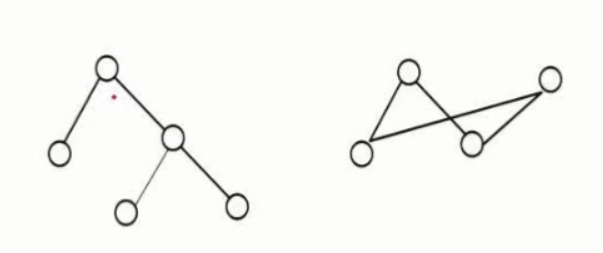
非线性结构(树形结构:无环路,图:有环路)
1、线性表的概念
(a1,a2,,a3)
2、线性表常见的两种存储结构
顺序存储结构(顺序表)
链式存储结构(链表)
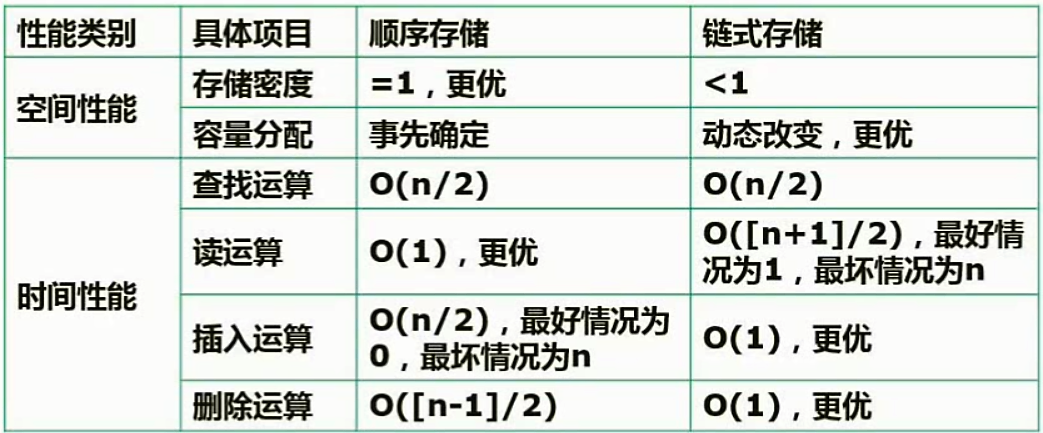
线性表顺序表

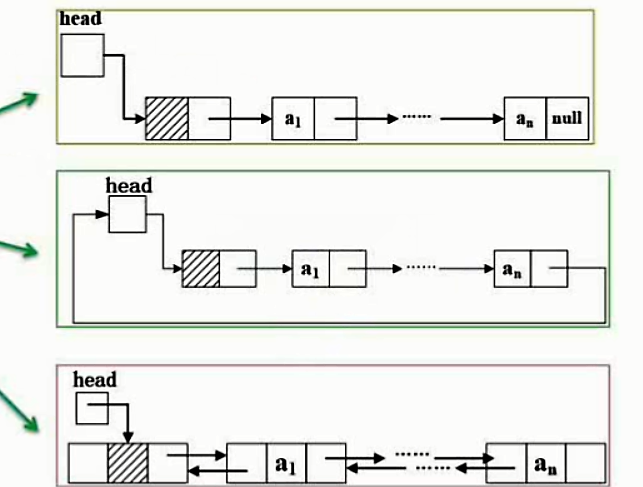
链表
单链表
循环链表
双向链表
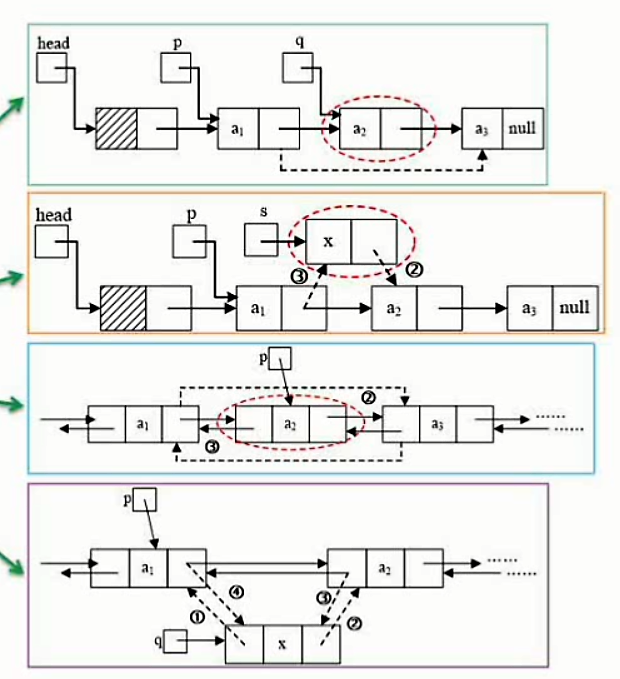
单链表删除结点
单链表插入结点
双向链表删除结点
双向链表插入结点
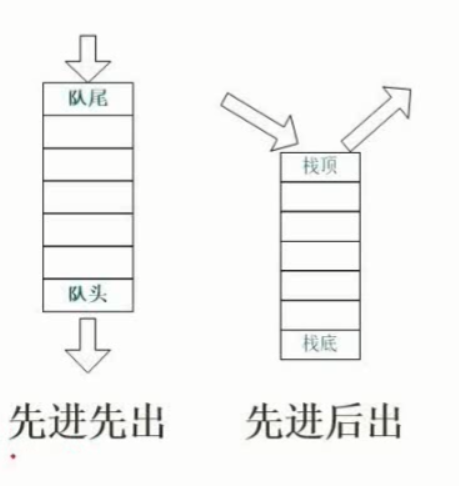
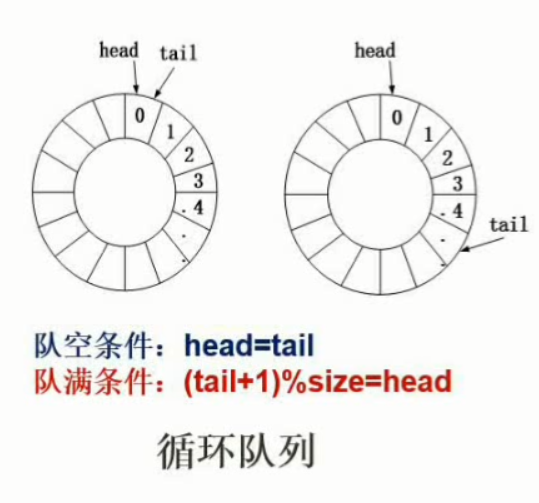
例题

A:e4,e3,e2,e1
B:e4,e2,
C:e4,e3,e1,e2
D:e4,e2,e3,e1
广义表广义表是n个表元素组成的有限序列,是线性表的推广。
通常用递归的形式进行定义,记做:LS(a0,a1,.,an)。
注:其中LS是表名,ai是表元素,它可以是表(称做子表),也可以是数据元素(称为原子)。其中n是广义表的长度(也就是最外层包含的元素个数),n=0的广义表为空表;而递归定义的重数就是广义表的深度,直观地说,就是定义中所含括号的重数(原子的深度为0,空表的深度为1)。
基本运算:取表头head(Ls)和取表尾tail(Ls)。
若有:LS1=(a,(b,c),(d,e))head(LS1)=atail(LS1)=((b,c),(d,e))树与二叉树
结点的度
树的度
叶子结点
分支结点
内部结点
父结点
子结点
兄弟结点
层次
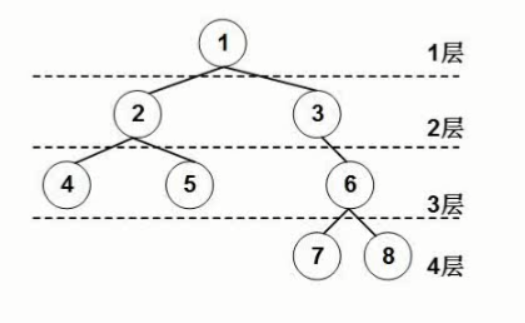
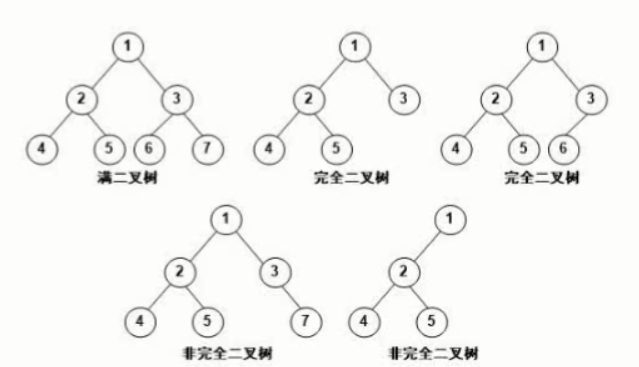
二叉树的重要特性:
在二叉树的第i层上最多有2^i-1个结点(i=1);
深度为k的二叉树最多有2k-1个结点(k=1);
对任何棵二叉树,如果其叶子结点数为n0,度为2的结点数为n2,则n0=n2+1。
如果对一棵有n个结点的完全二叉树的结点按层序编号(从第1层到log2nJ+1层,每层从左到右),则对任一结点i(1=i=n),有:
*如果i=1,则结点i无父结点,是二叉树的根;如果i1,则父结点是【i/2】;
*如果2in,则结点为i叶子结点,无左子结点;否则,其左子结点是结点2i;
*如果2i+1n,则结点无右子叶点,否则,其右子结点是结点2i+1。
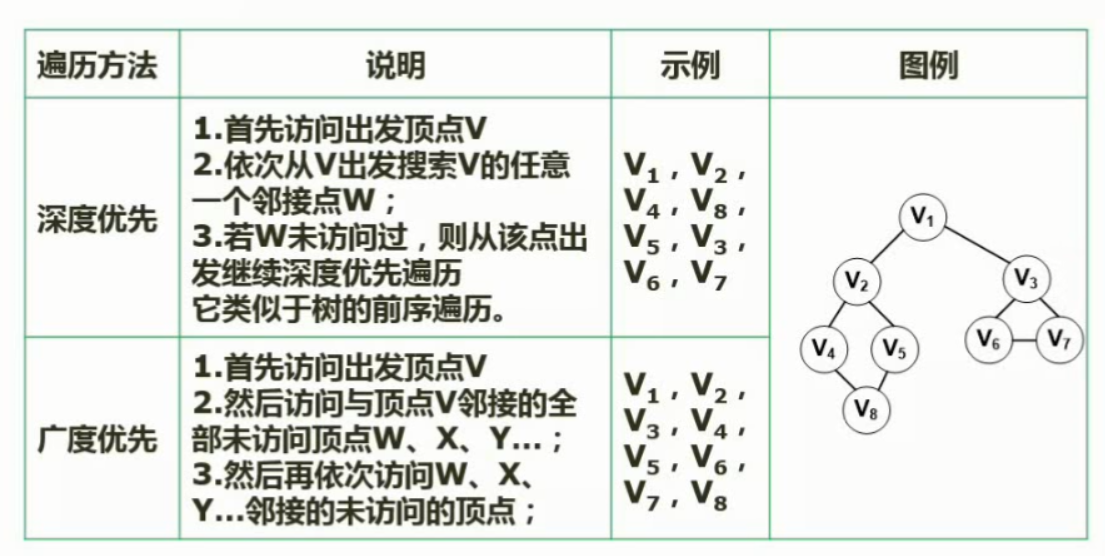
树与二叉树遍历前序遍历12457836
中序遍历42785136
后序遍历48752631
层次遍历12345678
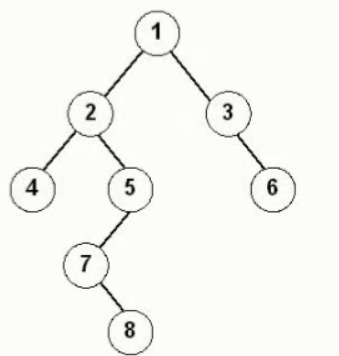
由前序序列为ABHFDECG;中序序列为HBEDFAGC构造二叉树。
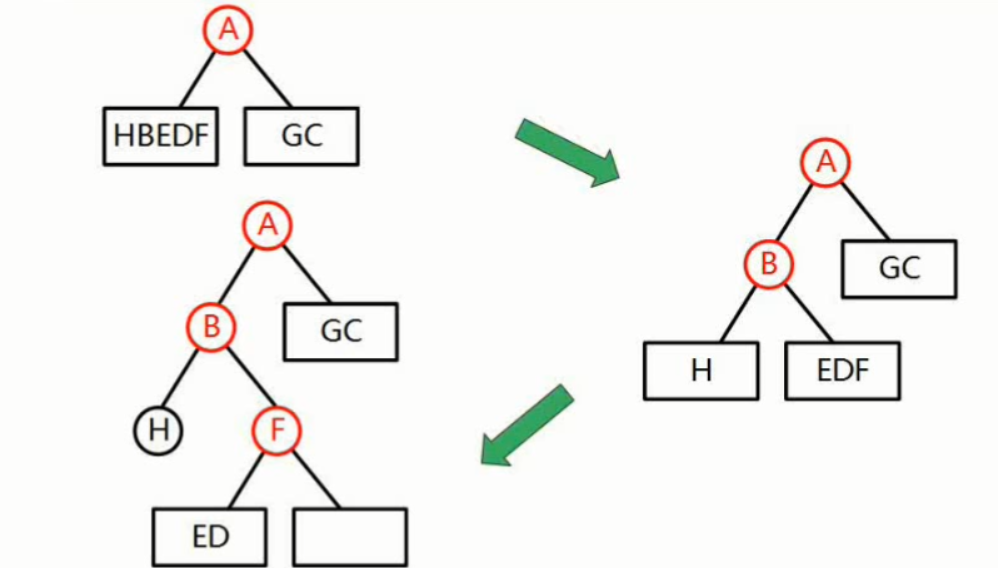
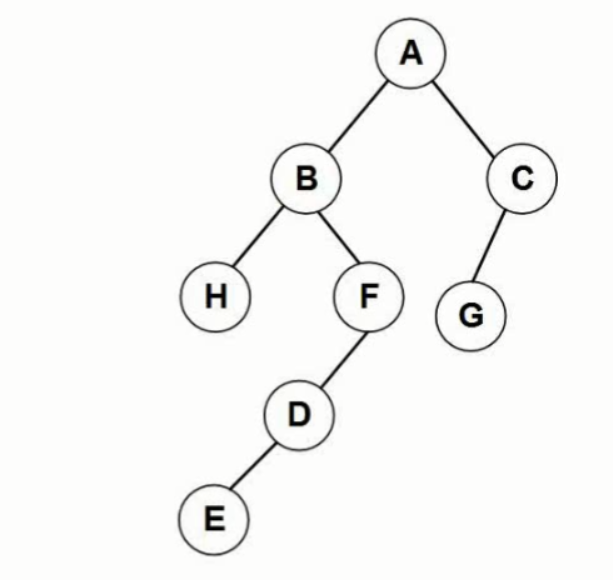
孩子结点-左子树结点
兄弟结点-右孩子结点
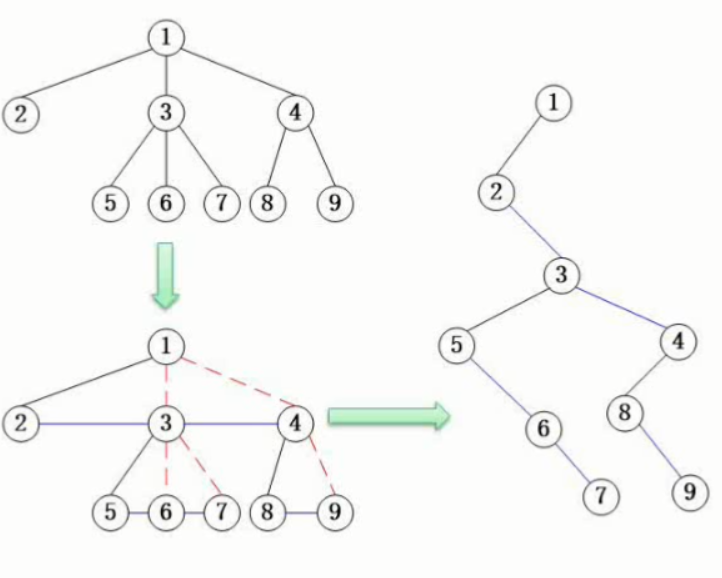
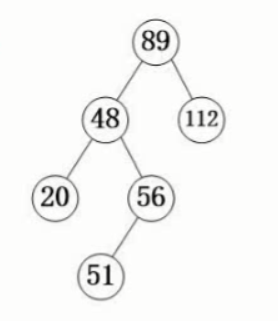
二叉排序树
左孩子小于根
右孩子大于根
(在多媒体的压缩方式经常使用:无损压缩)
需要了解的基本概念:
树的路径长度
权
带权路径长度
树的带权路径长度(树的代价)
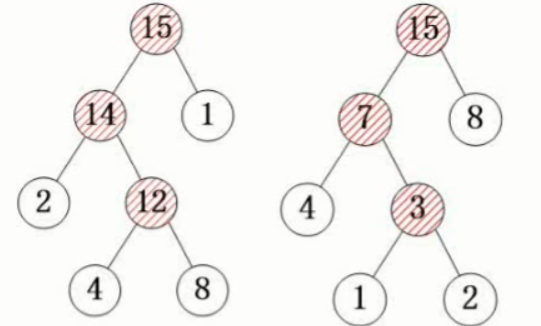
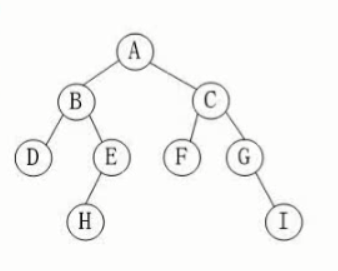
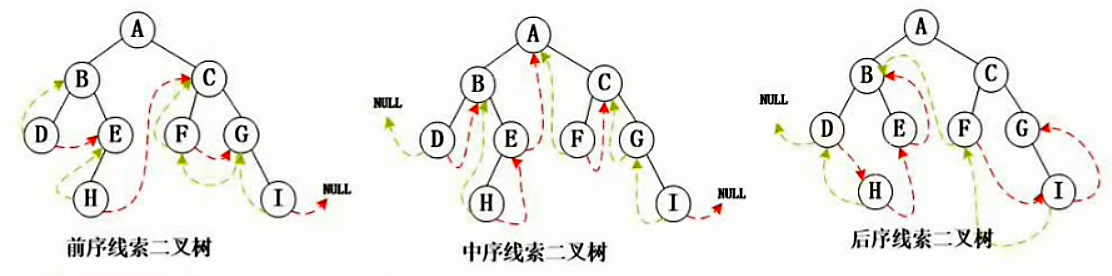
为什么要有线索二叉树
线索二叉树的概念
线索二叉树的表示
如何将二叉树转化为线索二叉树
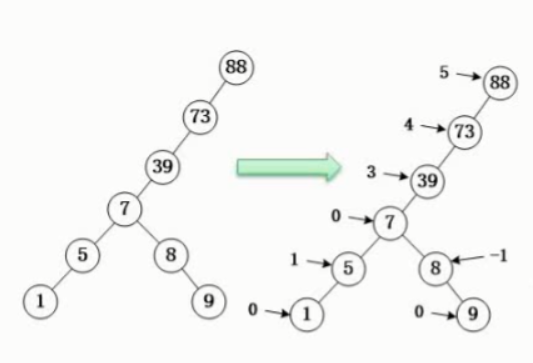
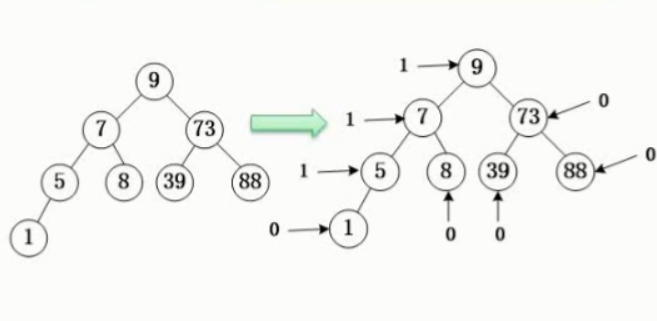
平衡二叉树的提出原因
平衡二叉树的定义(
任意结点的左右子树深度相差不超过1
每结点的平衡度只能为-1、0或1)
平衡树的建立过程
动态调平衡问题
完全图
在无向图中,若每对顶点之间都有一条边相连,则称该图为完全图(completegraph)
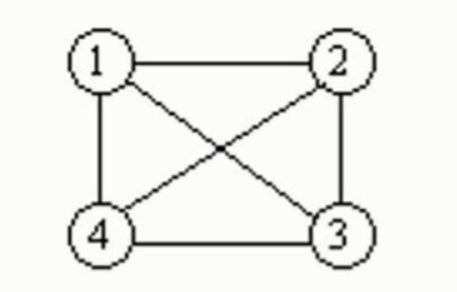
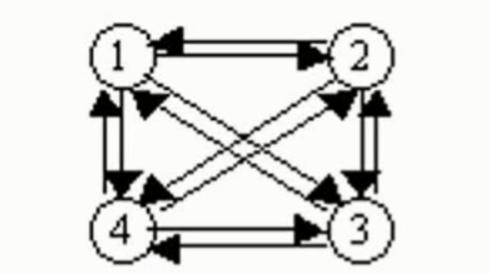
在有向图中,若每对顶点之间都有两条有向边相互连接,则称该图为完全图。

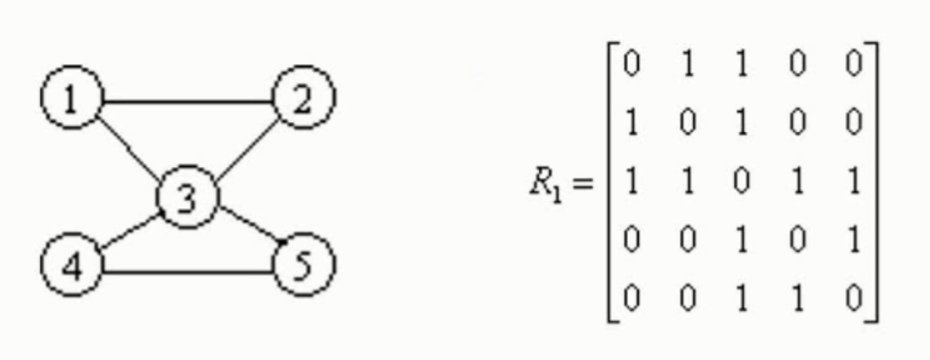
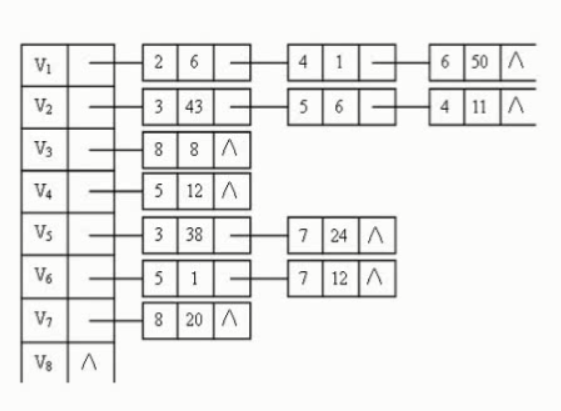
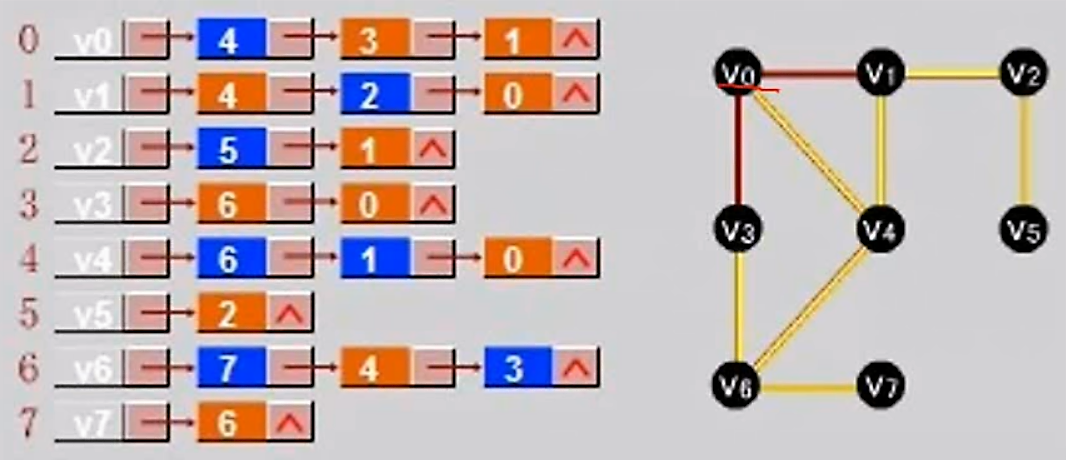
首先把每个顶点的邻接顶点用链表示出来,然后用一个一维数组来顺序存储上面每个链表的头指针。
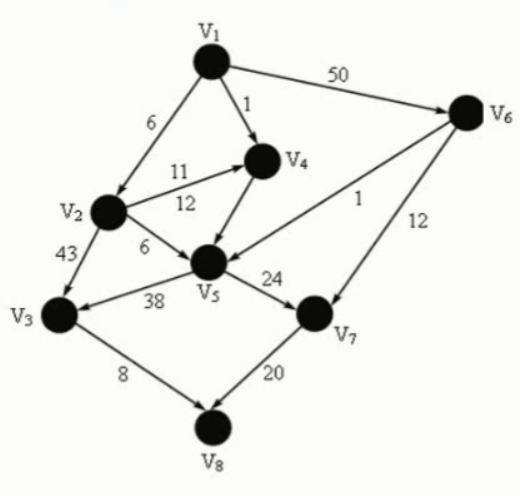
我们把用有向边表示活动之间开始的先后关系。这种有向图称为用顶点表示活动网络,简称AOV网络
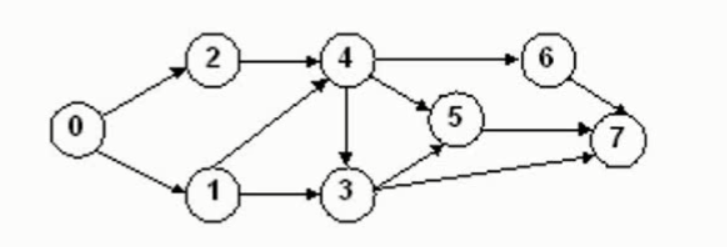
上图的拓扑序列有:02143567,01243657,02143657,01243567
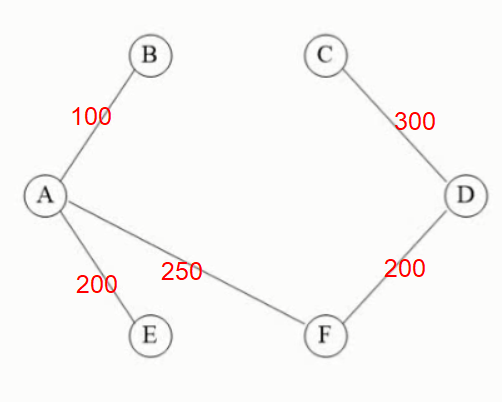
图的最小生成树-普里姆算法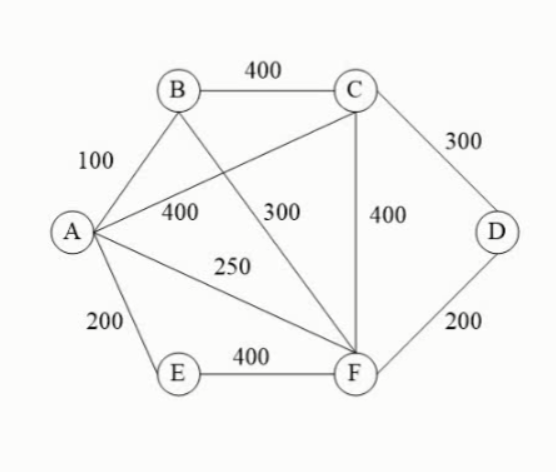
有穷性:执行有穷步之后结束
确定性:算法中每一条指令都必须有确切的含义,不能含糊不清。
输入(=0)
输出(=1)
有效性:算法的每个步骤都能有效执行并能得到确定的结果。例如a=0,b/a就无效。
算法基础-算法的复杂度时间复杂度:
如果存在两个常数c和m,对于所有的n,当n=m时有f(n)=cg(n),则有f(n)=O(g(n))。也就是说,随着n的增大,f(n)渐进地不大于g(n)。例如,一个程序的实际执行时间为T(n)=3n^3+2n^2+n,则T(n)=O(n^3).常见的对算法执行所需时间的度量:O(1)0(log2n)O(n)O(nlog2n)O(n^2)O(n^3)0(2^n)
空间复杂度:
查找-顺序查找顺序查找的思路:将待查找的关键字为key的元素从头到尾与表中元素进行比较,如果中间存在关键字为key的元素,则返回成功;否则,则查找失败。
查找成功时,顺序查找的平均查找长度为(等概率情况下):

二分法查找的基本思想是:(设R[low,..,high]是当前的查找区)
(1)确定该区间的中点位置:mid=[(low+high)/2];
(2)将待查的k值与R[mid].key比较,若相等,则查找成功并返回此位置,否则需确定新的查找区间,继续二分查找,具体方法如下。
●若R[mid].keyk,则由表的有序性可知R[mid,..,n].key均大于k,因此若表中存在关键字等于k的结点,则该结点必定是在位置mid左边的子表R[low,,mid-1]中。因此,新的查找区间是左子表R[low,..,high],其中high=mid-1。●若R[mid].keyk,则要查找的k必在mid的右子表R[mid+1,high]中,即新的查找区间是右子表R[low,..,high],其中low=mid+1。●若R[mid].key=k,则查找成功,算法结束。
(3)下一-次查找是针对新的查找区间进行,重复步骤(1)和(2)。
(4)在查找过程中,low逐步增加,而high逐步减少。如果highlow,则查找失败,算法结束。
例题:
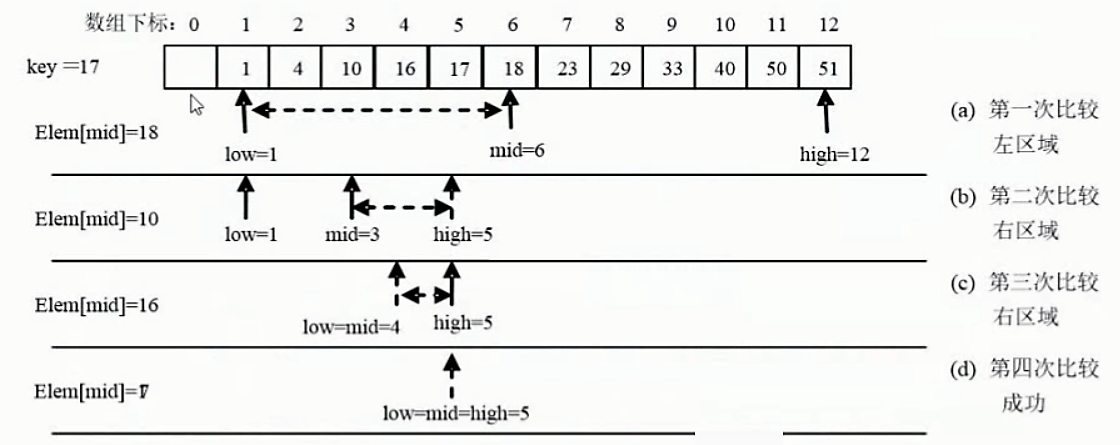
折半查找在查找成功时关键字的比较次数最多为[log2n]=1次。
折半查找的时间复杂度为O(log2n)。
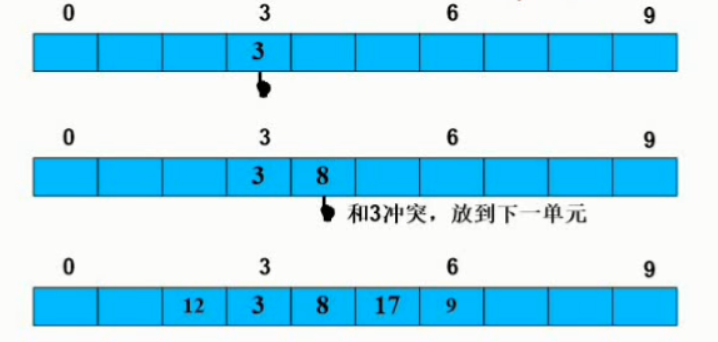
查找-散列表查找-散列表冲突的解决方法线性探测法
伪随机数法
1、排序的概念
稳定与不稳定排序
内排序与外排序
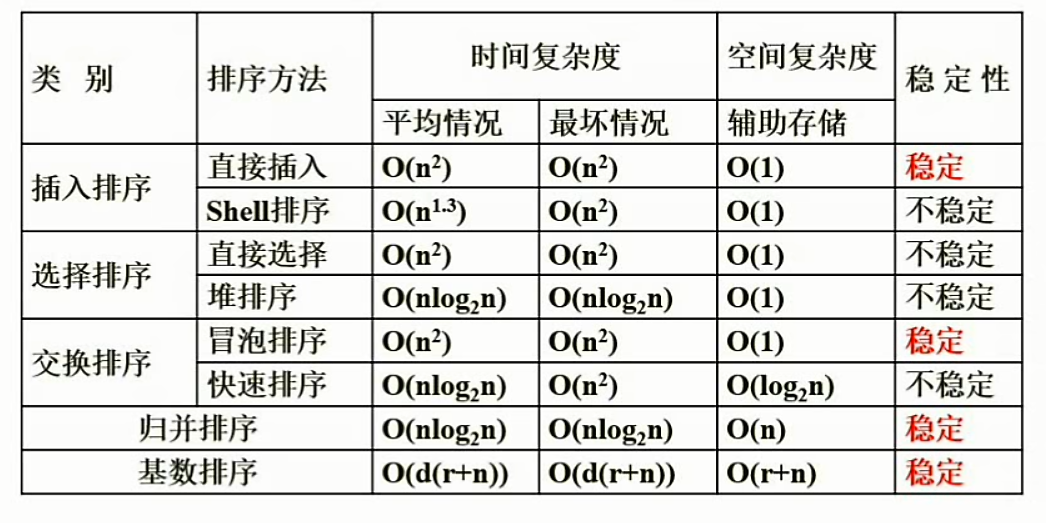
2、排序方法分类
插入类排序
(直接插入排序
希尔排序)
交换类排序
(冒泡排序
快速排序)
选择类排序
(简单选择排序
推排序)
归并排序
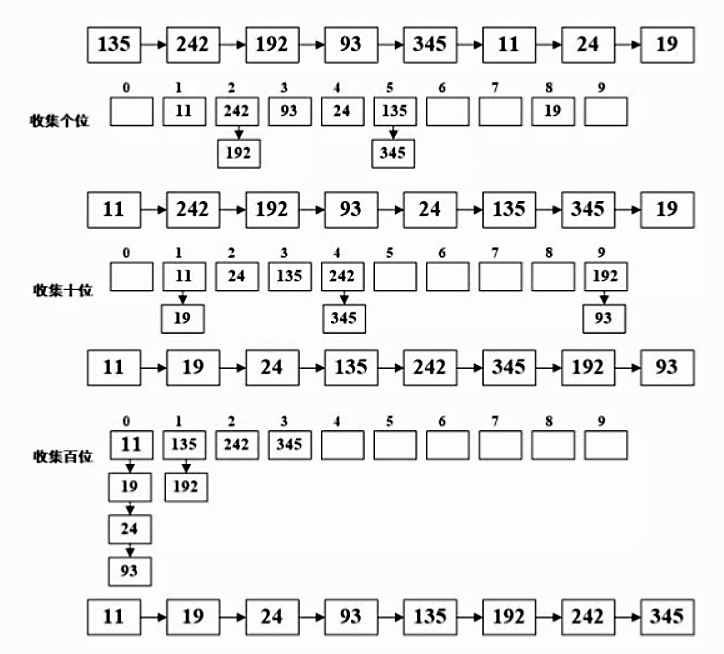
基数排序
排序-直接插入排序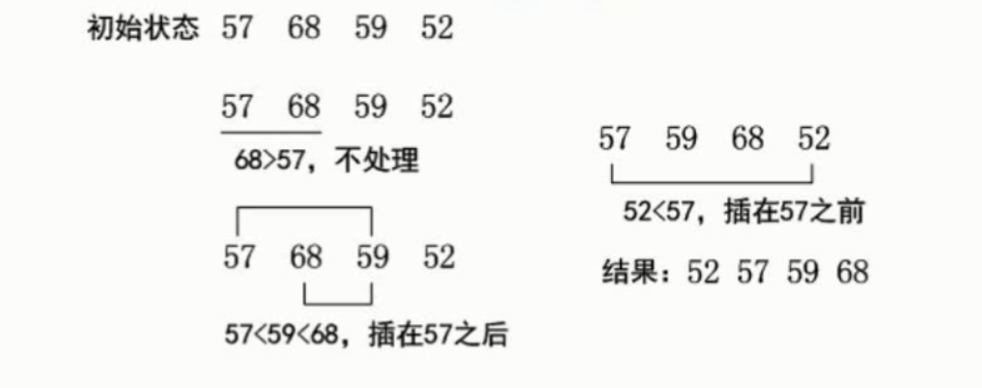
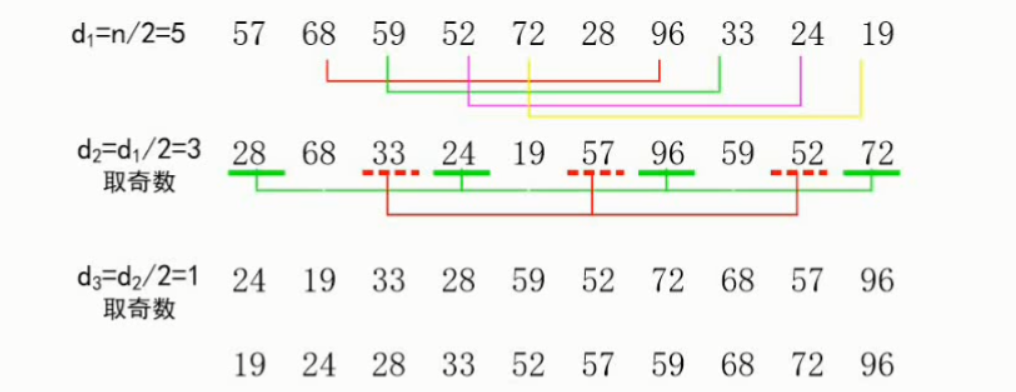

(最复杂的一种)
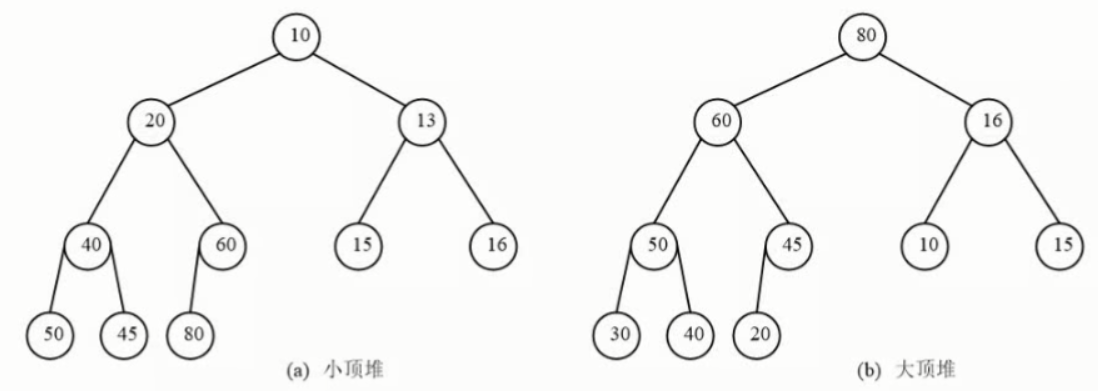
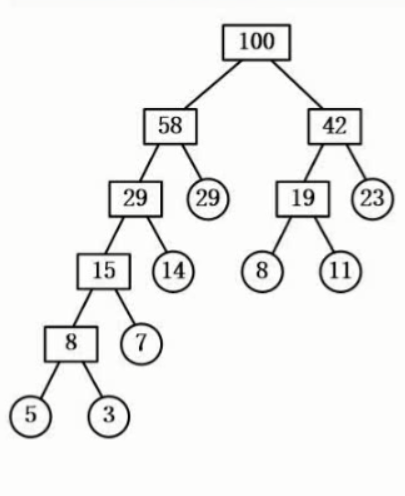
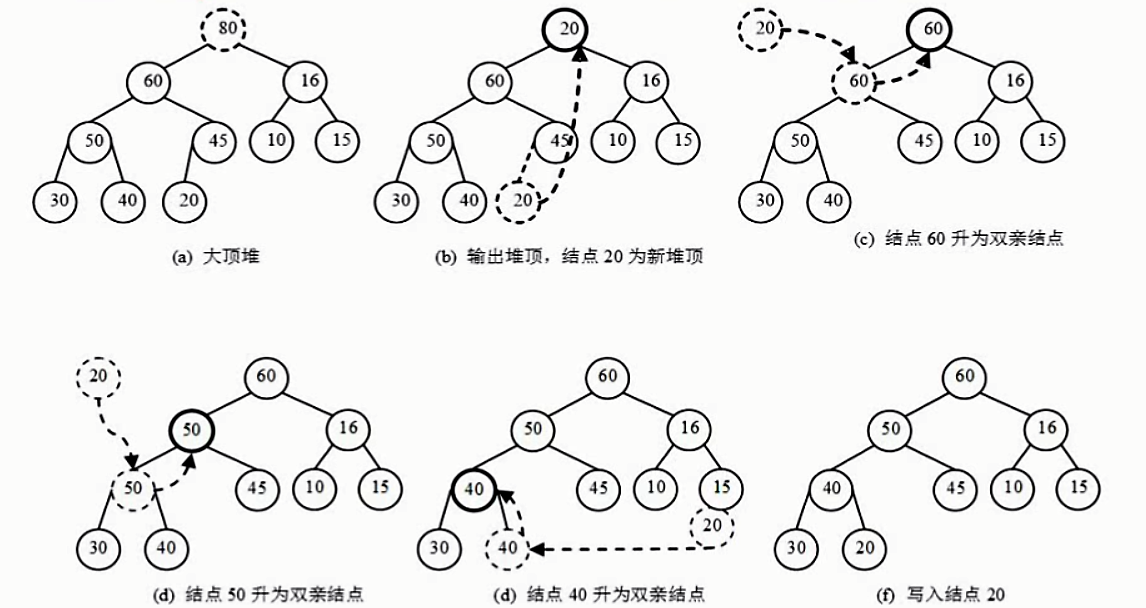
堆排序的算法步骤如下(以大顶堆为例):
(1)初始时将顺序表R[1..n]中元素建立为一个大顶堆,堆顶位于R[1]待序区为R[1..n].(2)循环执行步骤3~步骤4,共n-1次。(3)假设为第次运行,则待序区为R[1..n-i+1],将堆顶元素R[1]与待序区尾元素R[n-i+1]交换,此时顶点元素被输出,新的待序区为R[1..n-i]。(4)待序区对应的堆已经被破坏,将之重新调整为大顶堆。
例题:
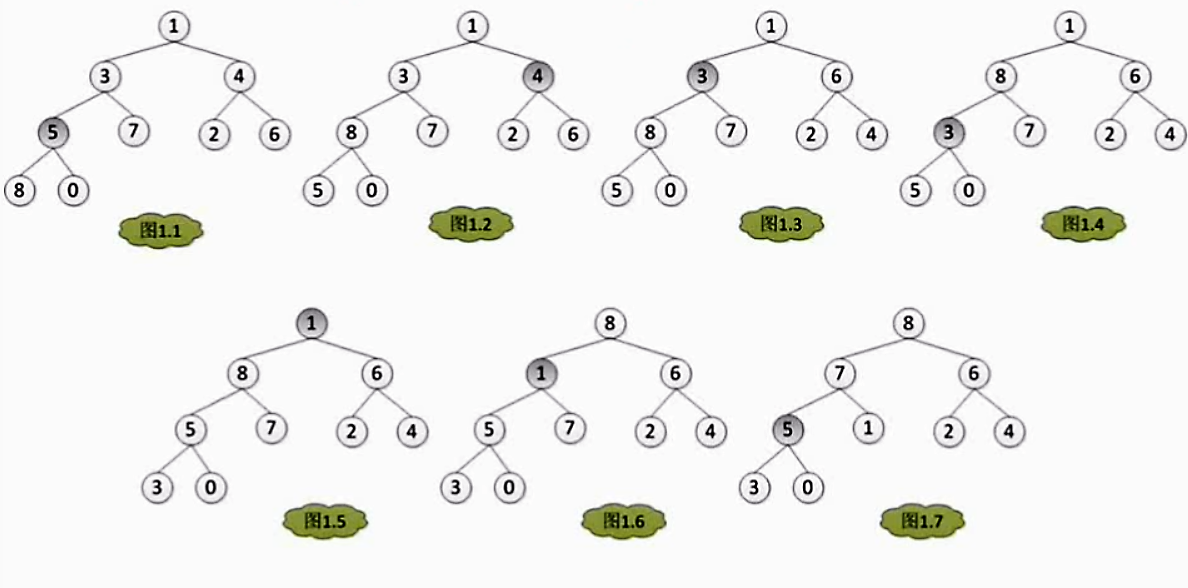
例题
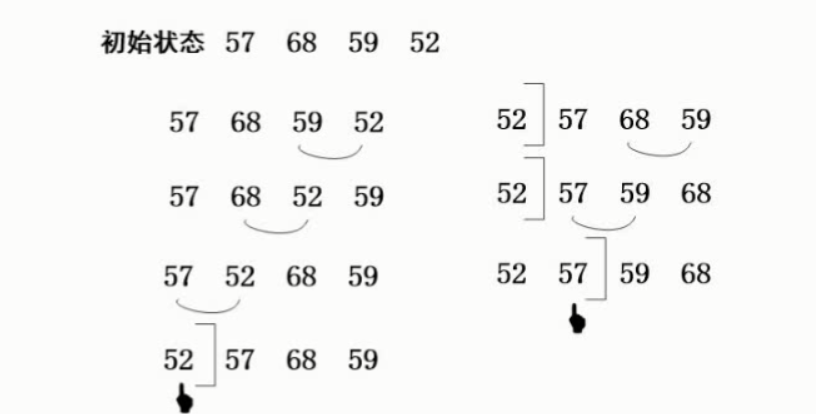
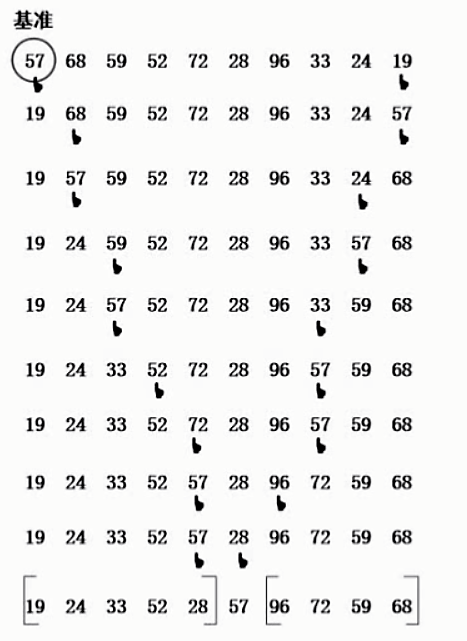
快速排序通常包括两个步骤:
第一步,在待排序的n个记录中任取一个记录,以该记录的排序码为准,将所有记录都分成两组,第1组都小于该数,第2组都大于该数,如图所示。第二步,采用相同的方法对左、右两组分别进行排序,直到所有记录都排到相应的位置为止。